HELP! Long Division
Today’s post is about long division - or as I like to call it…really big division.
I was recently talking to some upper grade teachers who were frustrated because their kids just weren’t getting long division. This was a combination of asking them to remember too many unconnected things and a lack of number sense with larger numbers (as always unfortunately!).
The kids were frustrated and of course, teachers too.
So I set out, as I always do, to break down the concept of long division to its necessary parts to build up to understanding what is happening.
Again, in reality, very few of us adults are out in the world doing long division. We have a phone with a calculator that is just so much faster. So if I can sweat less about them being able to do it and focus more on them understanding, diving deeper into the number system, and logically solving problems on the way…that’s where I will start.
So what prerequisite skills do students need to tackle large division?
Place Value, including flexible place value.
It no longer shocks me when I dive deep into a concept and realize that the breakdown starts when we abandon place value. We usually do kids a disservice by not emphasizing this skill more and not applying it to larger and larger numbers as they move up.
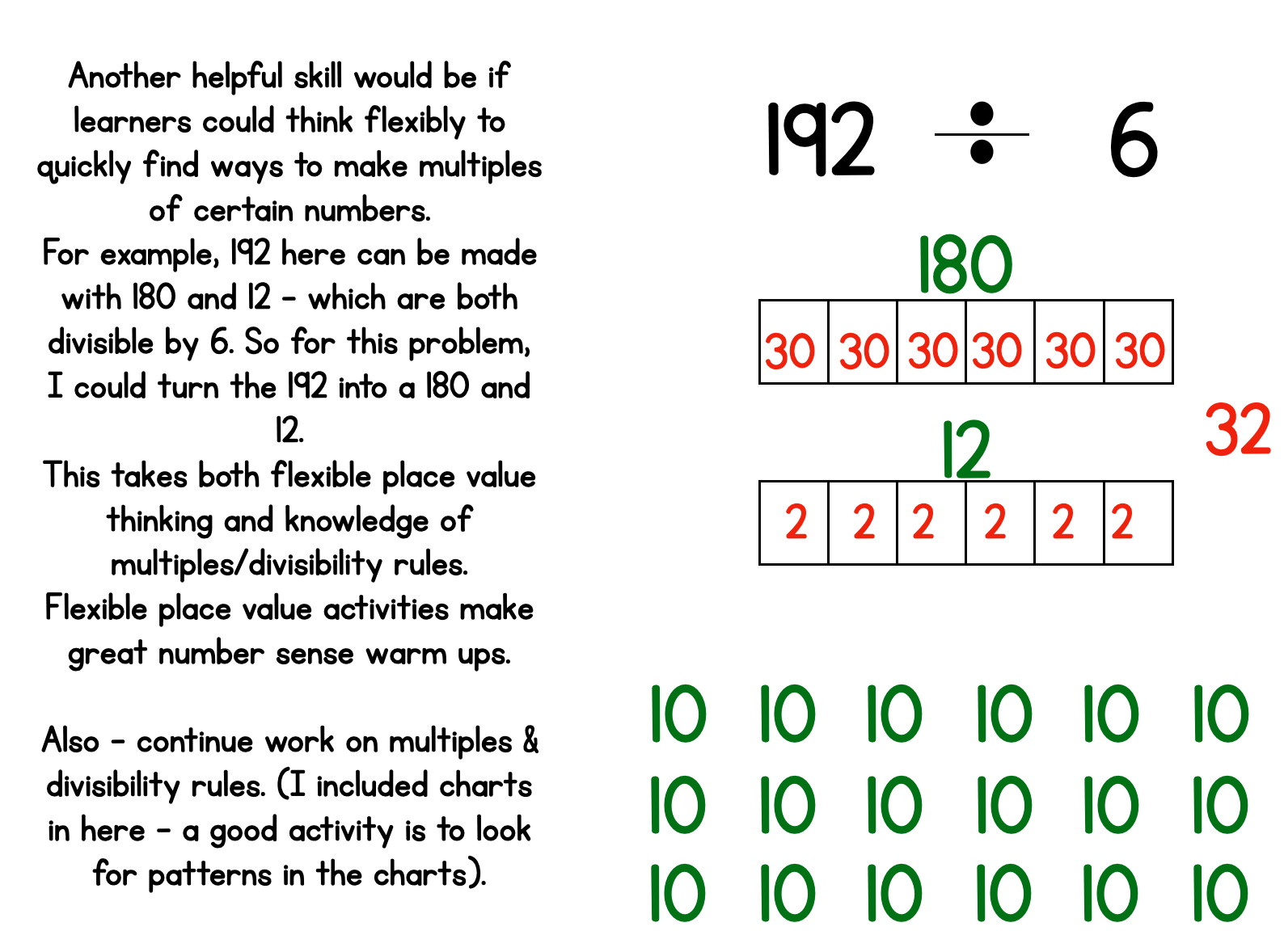
Students need to be able to break a large number into it’s parts and in flexible ways. For example, 184 is 100 + 80 + 4, and also 180 + 4, and also 160 + 24.
Some quick flexible place value warm-up activities will help learners break numbers apart in this way.
2. Division Connections
It’s obvious that learners need strong single division skills for large division, but part of this is making
connections from small division problems to large division problems.
3. Multiples, Multiple, Multiples!
I touched on this in number 1, but after students are able to break numbers flexibly with place value, they
will need to be able to find what numbers to use. This means they need to know their multiples - well into
the hundreds.
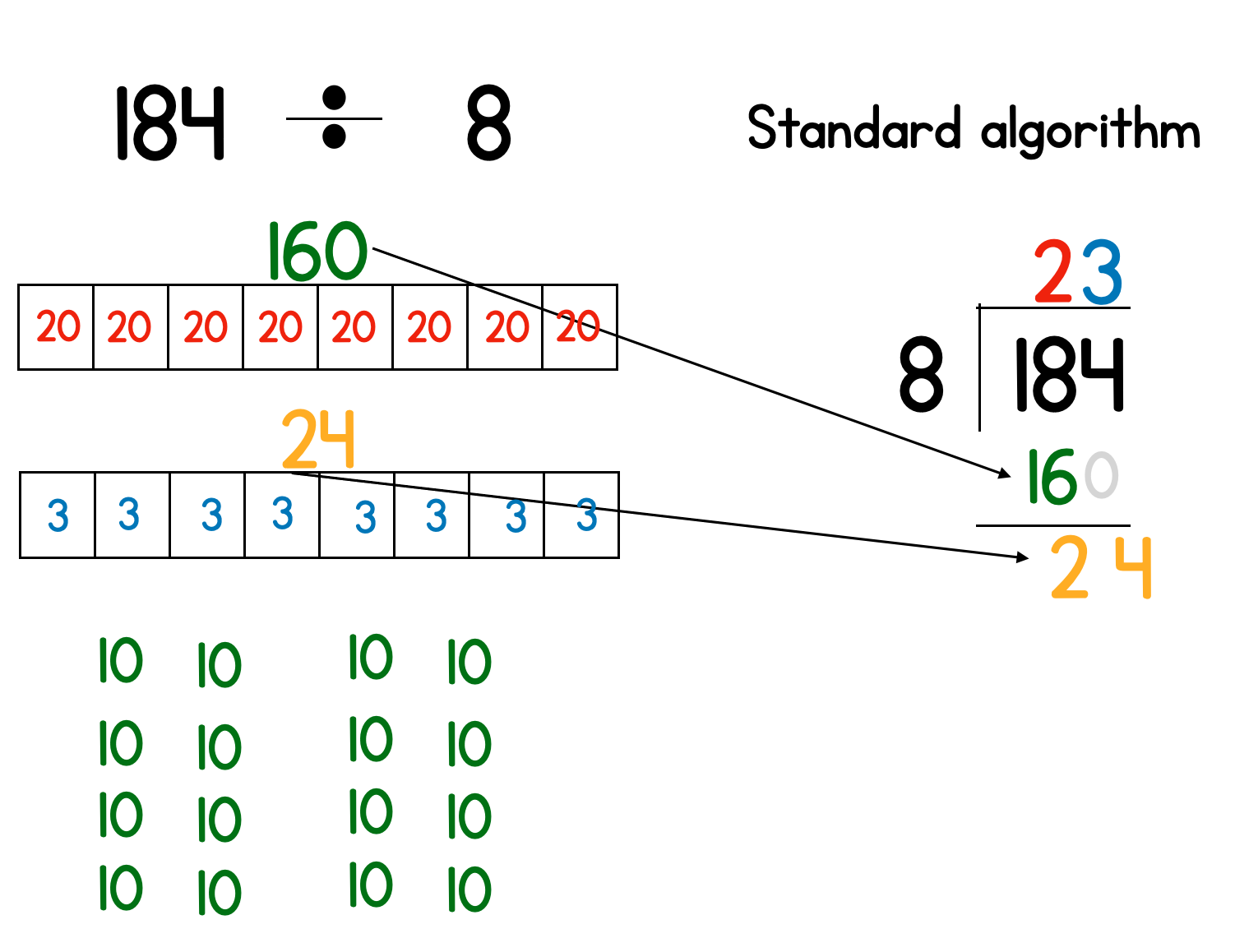
For example, let’s look at 184 divided by 8. Using flexible place value, I know I can break 184 into 160 and
24. If I know my multiples of 8 I will know I want to do that instead of 170 + 14 or something else.
From there, I can divide 160 by 8 using what I know about 16 divided by 8. Then 24 divided by 8.
You can see here how that is exactly what is happening in the standard algorithm.
Hopefully these steps give you some ideas to help scale your students up to LARGE division!