Let's dive into the fascinating world of fractional and decimal thinking! This concept is introduced early on in mathematics education, and it becomes even more significant as students progress through upper elementary grades.

Screenshot 2023-06-24 at 11.17.14 AM.png

Screenshot 2023-06-24 at 11.16.35 AM.png

Screenshot 2023-06-24 at 11.16.23 AM.png

If you're new here, you'll find that this post is all about developing a conceptual understanding of fractional and decimal concepts. In my approach, I prioritize deep comprehension over the ability to quickly arrive at correct answers or follow strict formulas and rules. Instead, I emphasize the importance of using strong visuals and engaging in problem-solving activities to help students truly grasp the intricacies of fractions and decimals. By building a solid foundation of understanding, students will be equipped to apply their knowledge effectively in real-world situations.

As teachers, we need to be sure our students develop a solid understanding of the whole number system before jumping into fractions. A strong foundation in whole numbers will help students avoid struggle and misconceptions with fractional thinking.

Remember, when students are learning a number system they need to practice components of numeracy like:

counting
recognizing (subitizing)
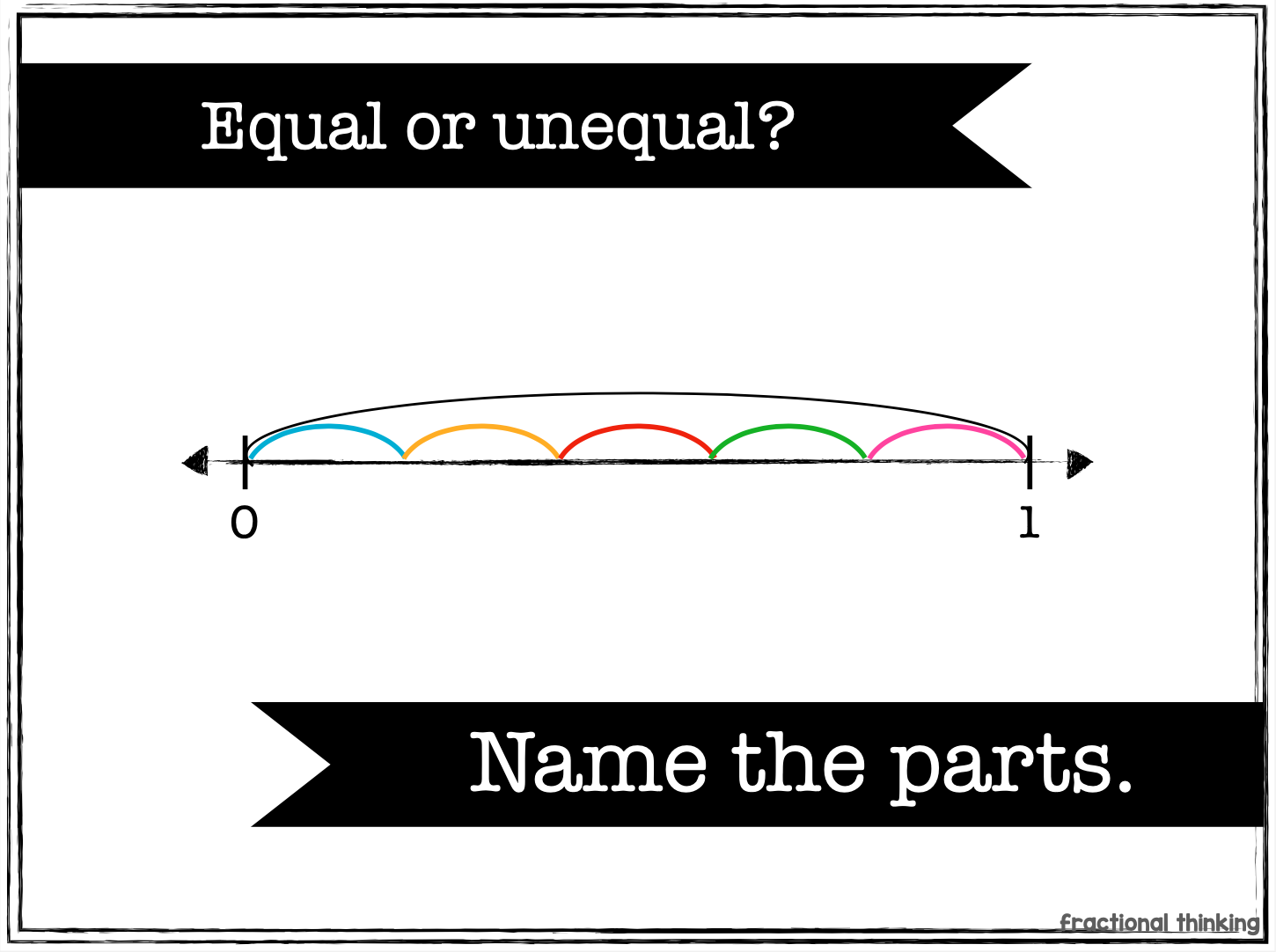
representing
ordering/comparing

Once students have a strong foundation in whole numbers, they can confidently delve into fractional and decimal numbers. These numbers represent parts of a whole or portions of a group of wholes. However, before exploring fractions and decimals, it is crucial for students to grasp the concept of a whole. They need to understand what a whole looks like and be able to identify it in different contexts.

By ensuring students have a solid grasp of whole numbers, we set them up for success in developing their fractional and decimal thinking. This strong foundation will enable them to confidently navigate the world of numbers and confidently explore the concept of parts and wholes.

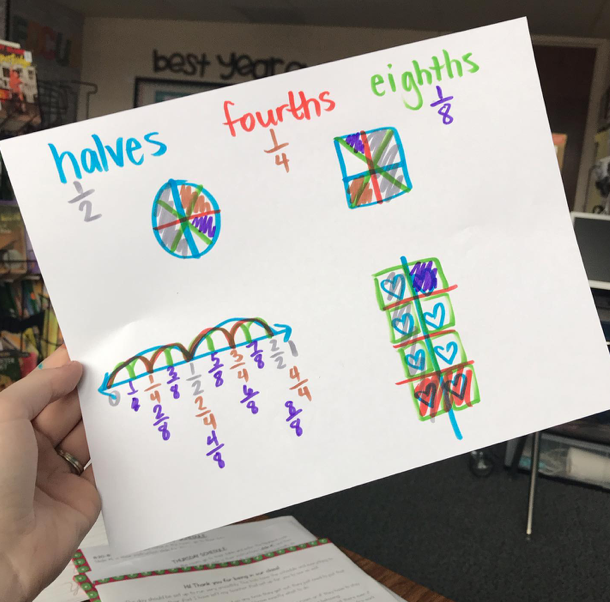
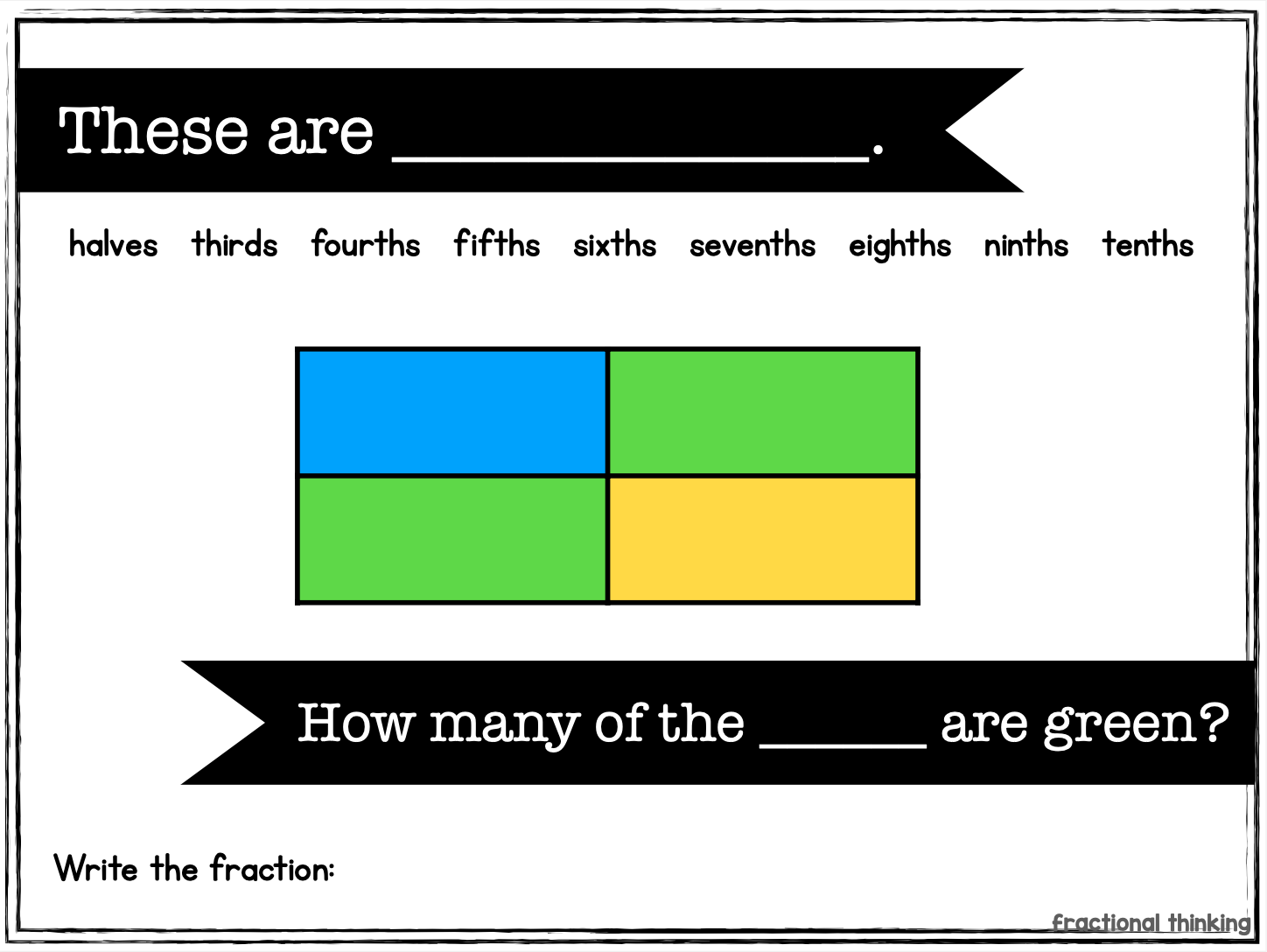
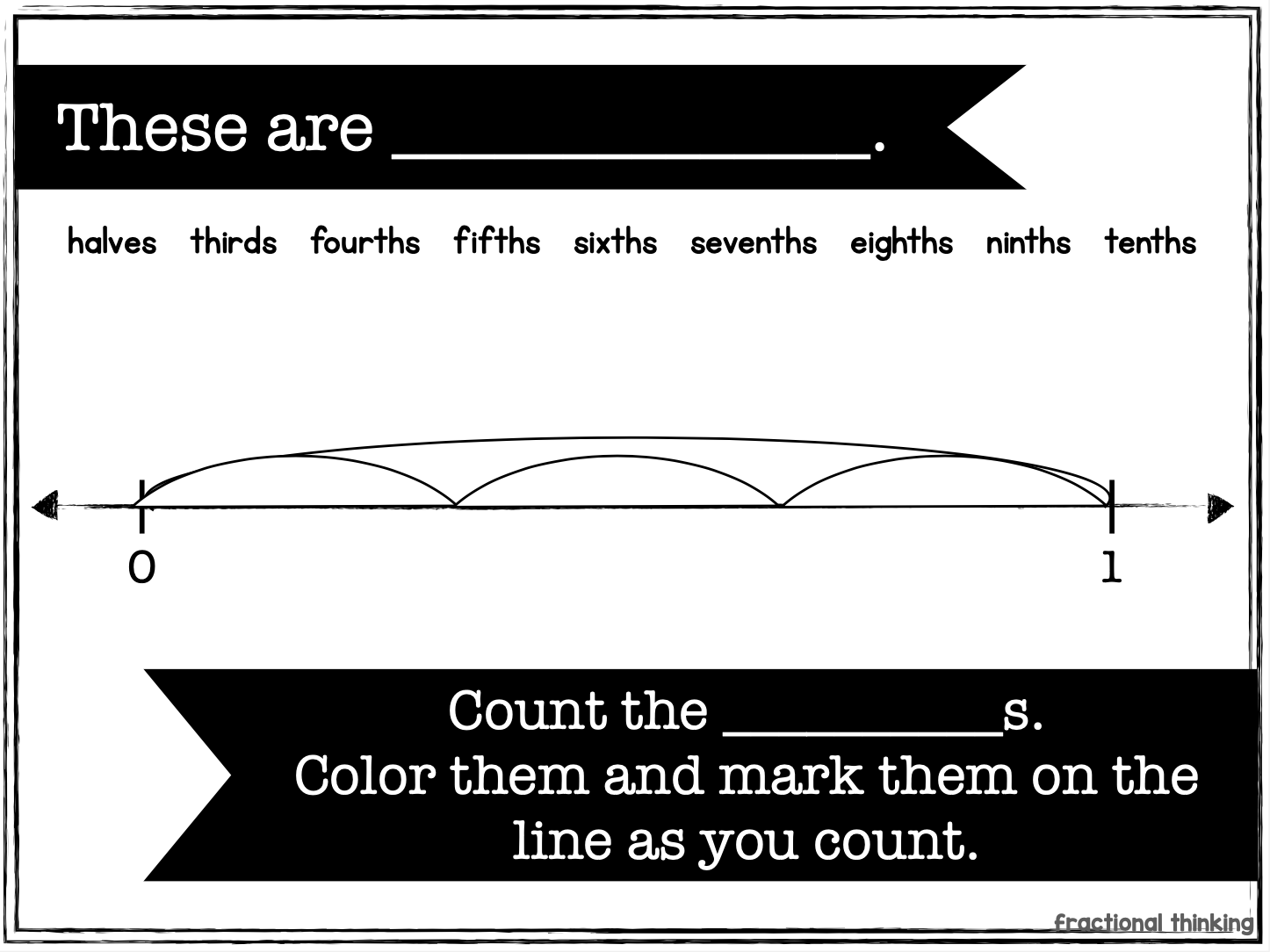
A fraction is a part of that whole. The names for the parts depend on how many parts there are.

These parts can be counted and represented. If there are 2 eighths represented in the visual, we call that two eighths and write it as 2/8.

A decimal is also a part of that whole. The names for the parts depend on how many parts there are.

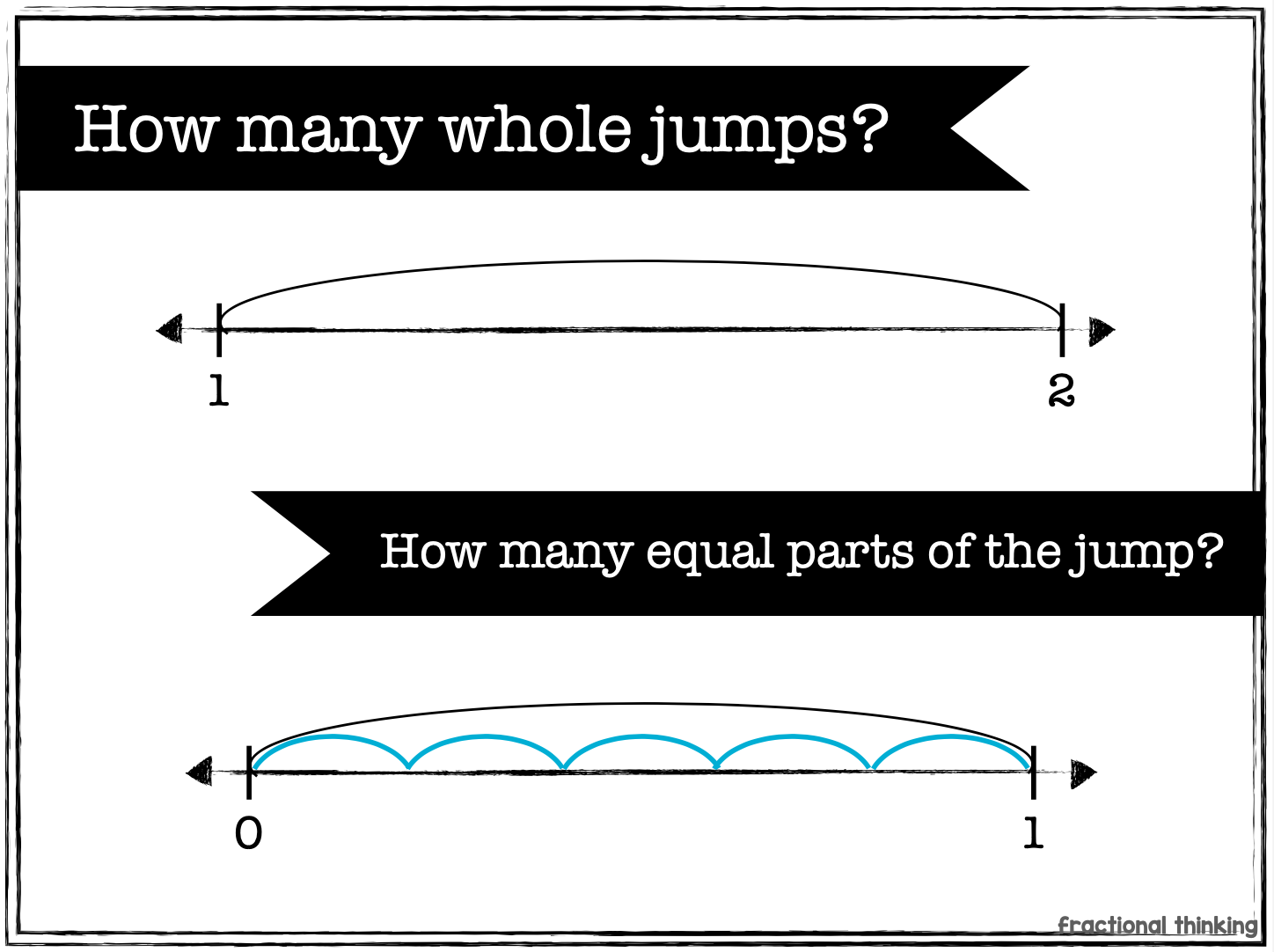
Just like whole numbers, these fractional/decimal part numbers can be counted. It’s always good to start with a visual as you’re counting.

For example, we can count 1/5, 2/5,/ 3/5, 4/5,/ 5/5. Each time we are adding a fifth. A fifth is what we call a part when there are five parts. This idea of '“fifths” being their own thing (unit) is important when you start adding fractions. You can easily add 2 fifths and 1 fifth because fifths are fifths. Just like adding 2 apples and 1 apple is 3 apples, 2 fifth and 1 fifth is 3 fifths. The fifths don’t change.

When thinking about decimals, I usually show students that tens always have 2 parts, and tenths also have two parts. The decimal is like a part (place holder for the non-existent oneths) and then we have tenths, hundredths, thousandths.

There can be infinite amounts of parts between numbers but we use tenths and hundredths the most.

Tenths are the ten parts between numbers and hundredths are the hundred parts between numbers.

Decimals (and fractions) show us that there isn’t quite a whole number amount, but something in between. For example, if I have 7.3 seconds left on the clock, it’s not quite 7 but not 8.

Because our number system is built on tens/tenths, halfway between our numbers will be 5/.5. So halfway from 8 to 9 Is 9.5 (or 9 and a half).

Remember, when you’re starting work with fractions and decimals, this is a brand new number system for students. They need time to play with it and they need to see it. Just like we use dot cards or cute object cards in kindergarten, we need visuals in upper elementary for these new numbers.

Most standards start with fractions in 2nd-3rd grade. We want to introduce students to parts within numbers with something concrete. Let’s look at some slides I would use to introduce fractions.

Once students are able to count with, recognize, and represent fractions you start introducing decimals and comparing/converting.

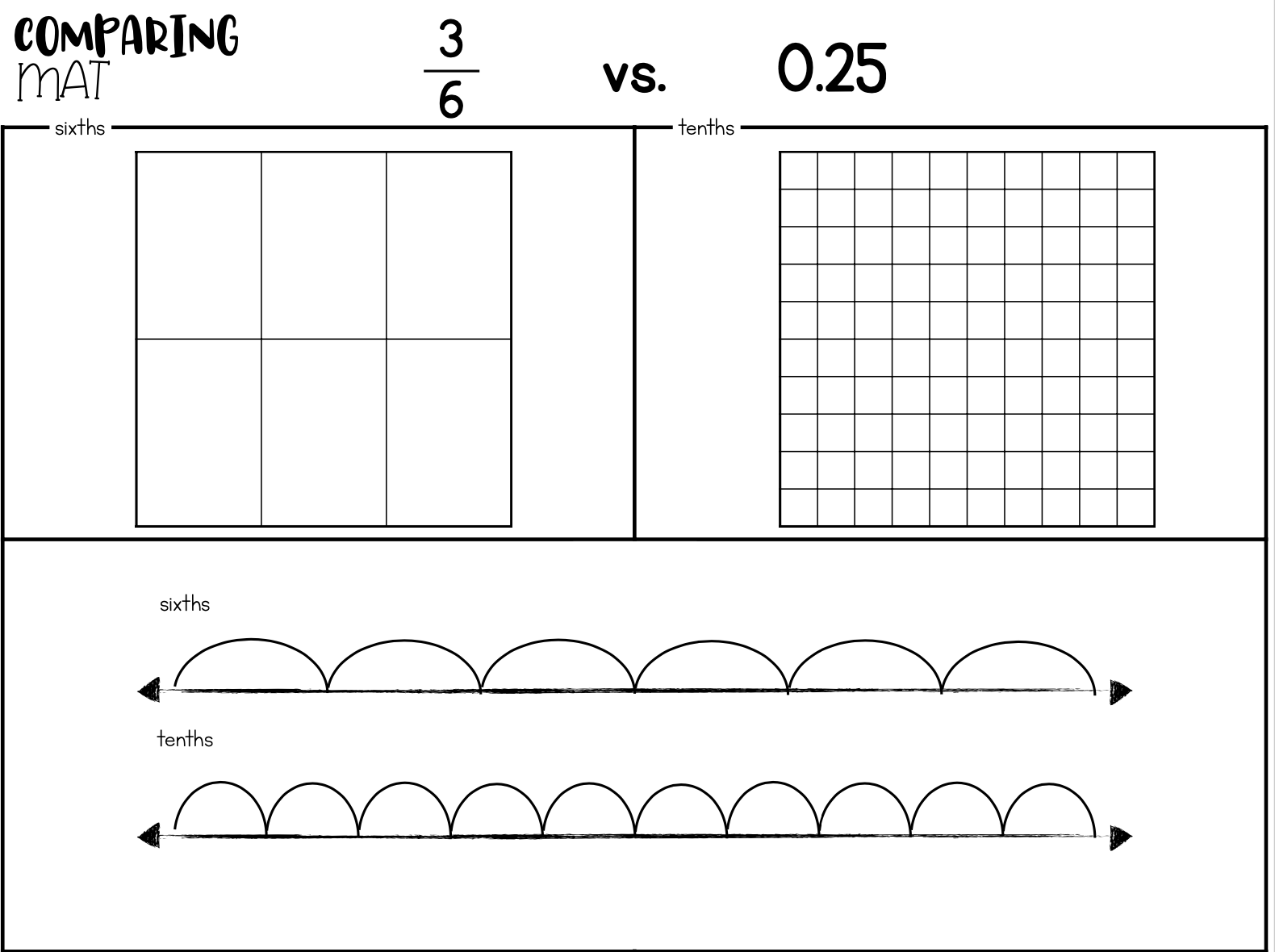
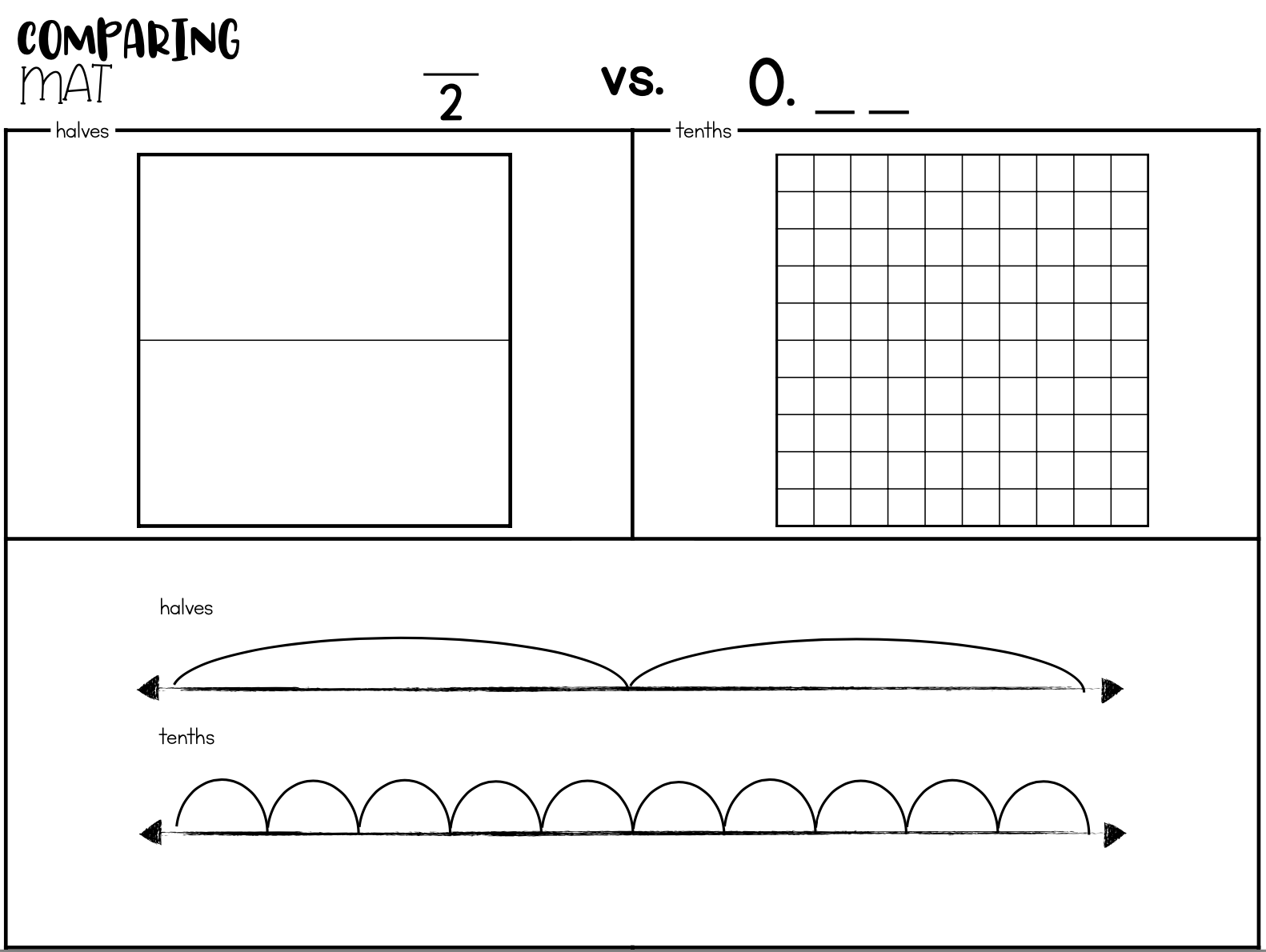
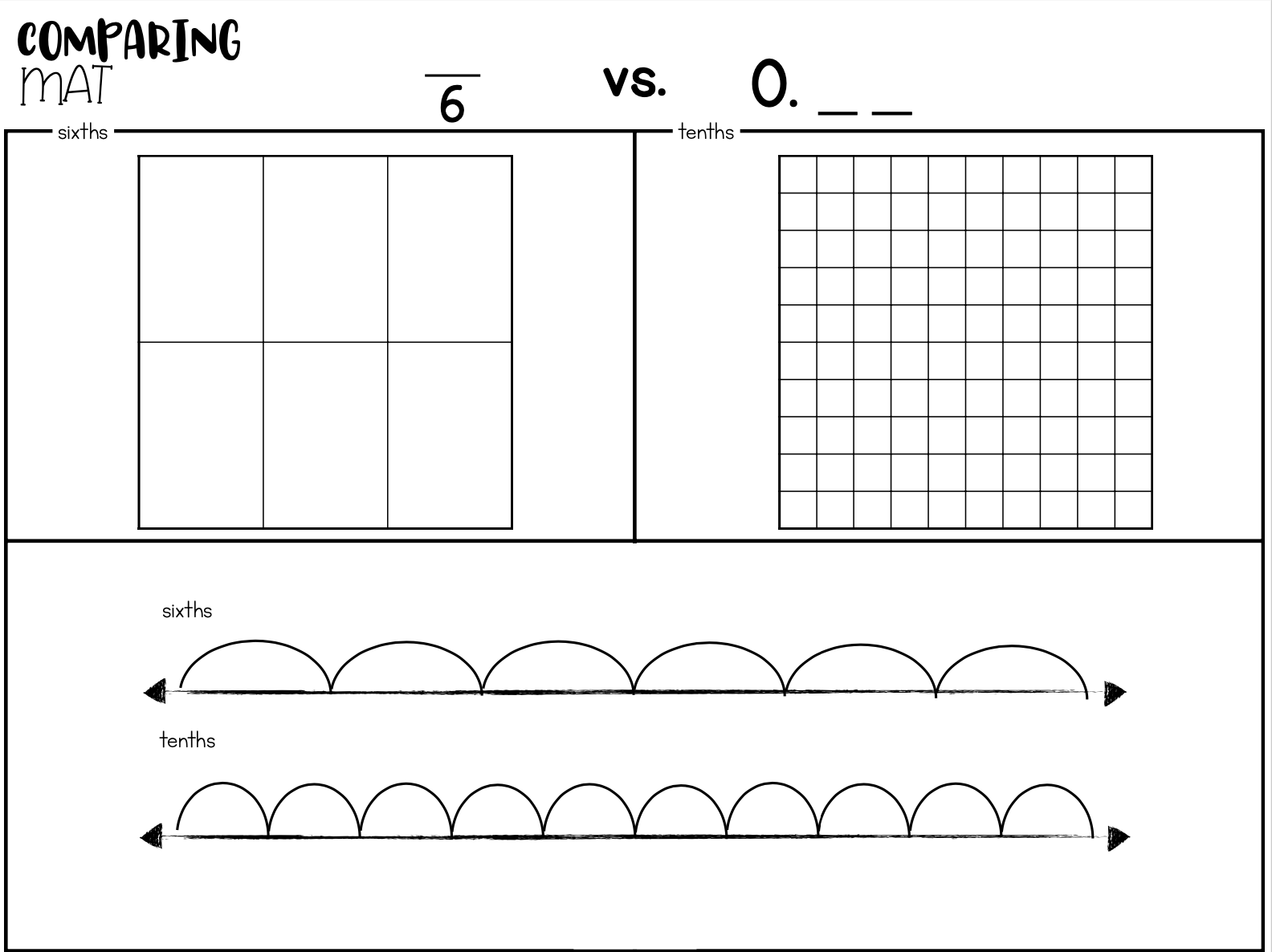
Decimal visuals include grids:

or number lines:

Once we have a good way to count, represent and recognize both fractions and decimals, we will look at them together. Always keeping our access to visuals so students can see the comparison.

Hopefully, they have success with this because they have had plenty of practice representing fractions and representing decimals - all they have to do is do both and compare!