multiplication strategies for 3rd grade

Hello, blogosphere!

Long time, no talk.

I'm not good with introductions so I am going to dive right into the content (which is what you came for anyway, right?) In 3rd grade, we are knee deep in multiplication and LOVING it (not a joke, not an exaggeration - we LOVE math in my class!) One of the major complaints I hear from colleagues, other teachers, and even parents is that their kids just aren't GETTING their facts. And when I probe or dig deeper, they usually mean they aren't memorizing them.

Which, could be a problem. But is most likely the symptom of a deeper problem.

Lack of understanding.

Other teachers that get this stand-up and say things like

"My kids totally GET multiplication. They draw out their groups and count them up."

This is better. I totally believe that students should understand multiplication anything before they move toward memorization. I am all for circles and stars, the 4 ways to show multiplication (number lines, skip counting, etc. - we use all these in my class). BUT (did you see that coming?) at some point students need to move toward strategies (hopefully mental) that help them arrive at facts without the need for drawings or number lines.

Often times we go straight from circles with dots to flashcards. We miss that middle ground where students are really building strategies to recall facts permanently. 

Rote memorization may get them to recall for now, but it is not a strategy.

Do I need to say that louder for the people in the back?

When I was researching these strategies, something that often happens to me came up. I was learning strategies that were never taught to me as a kid. And I was getting better at multiplication - as an adult! For example, a strategy for x9 would be to multiply the number by 10 and then take that number away. Here is a visual I use to show my kids.

We fill in the bottom part, 6 tens is 60. Then I tell them to "turn the tens into nines". They cross out one block from each ten. That leaves us with 60 - 6. Eventually, students begin to notice the pattern (20-2, 30-3, 40-4, 50-5, 60-6, etc.)

I NEVER learned that. Well into my college and adult life I would try to count by 9's all the way up to the answer. Was it effective? Usually, yes. Was it annoying? YES. I struggled with my 9 facts and now I get this quickly. 

My kids do too.

Intrigued? Good. I'm going to walk through the routine we use when learning a new strategy and then all the strategies I use with my kids and include visuals for how I introduce them. AND they are in the order I introduce them to kids. Good, yeah?

I pose problems to the kids in a simple table like this:

Most of the time they come to a conclusion themselves!

Then we can name the strategy, practice it, and add it to our charts!

Here are the strategies: 

1. x0 and x1

I highly suggest you lump these together because the time it'll take your kids to catch onto x0 will be laughable (if not, there's a bigger problem). 

For these, I do use the good old circles and stars method (linked here if you have no idea what I'm talking about). We fill in an organizer (I do this for each multiplication fact we go through) until students get the pattern and can express it. Then, I add it to our anchor chart. 

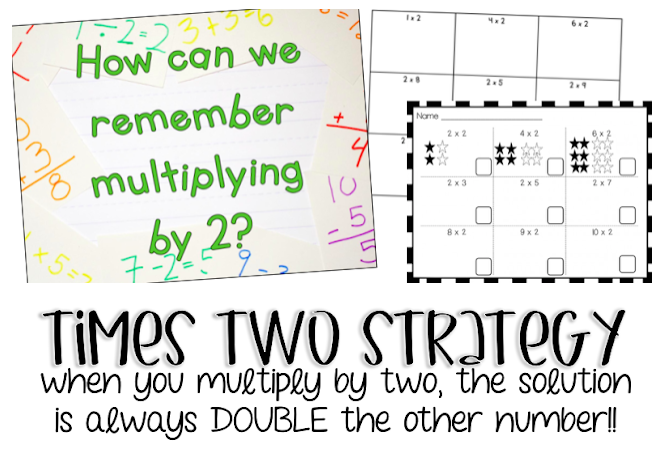
2. x2

From there, we move onto x2 or as we call it in my class - DOUBLING! (My kids love to shout this out for whatever reason but it sticks!) This was the point I realized my students were desperately behind on their doubles facts (ahem, why they are important!) but through our x2 lessons, they got them down. I would suggest going over them a lot or learning the rap (at least show it). Maybe that'll be just enough to trigger kids memory and get them used to DOUBLING. Again, we fill in an organizer and I hope that students begin to notice all the numbers are EVEN (we add any valid notices to the anchor chart). Now, anytime there is a x2 problem, I just point to the 2 and the kids say "DOUBLE it" and they're all over it. 

3. x5

I go to the 5 facts next. This is a natural progression because kids know how to count by 5's. This is also a good time to pull out your old clock and make some good connections (in case you forgot, analog clocks count by 5's.)

I give each student a clock on a paper (well, we actually do it on Nearpod and iPads but you could use paper) and we go around the clock counting by 5's. I then show students how the clock actually gives them x5 answers. If the problem is 4 x 5 we can look at the 4 on the clock and see the 4 really stands for 20. 4x5=20. For this reason, my kids call the 5 facts the clock facts. They love to take their clock and do a quiz, quiz, trade asking other students x5 facts. 

We add to our chart that all of these end with 0 or 5.

4. x10 

Multiplying by 10 is about the same process - students know how to count by 10's (we hope) and groups of 10's. Again, we do enough until I hope students begin to notice that you keep the number and add a 0. I only want that connection to happen after I am sure they understand they are counting by 10's/groups of tens. 

All of these end with 0.

5. x9

I do the 9's strategy right after the tens because we use our tens to do it! Again, I use base ten rods like in the picture. We create tens, turn them into 9's and figure out the problem. Students arrive at the idea that it's just the number x10 minus the number (20-2, 30-3, etc.) so we add that to the chart. 

My students also noticed that all the 9's facts are similar in this way

(x2, x9) 18, 81

(x3, x8) 27, 72

(x4, x7) 36, 63

(x5, x6) 45, 54

They don't and won't quite understand why this is yet but it's a great thing to notice AND they begin to remember that all 9's facts have those digits. Some of them even do the "lower" fact and then just reverse it. Whatever works and makes sense, ya'll!

6. x3

After the 9's it gets a bit tricky. When it comes to 3, 4, 6, and 8 I suggest using VISUALS. Like, a lot of visuals.

The 3's strategy basically works like this.

You double it (remember that kids!?) and then add ONE more group.

when I first taught this, I began to realize my kids could internalize that but they had no idea why. OOPS. This is when I started using visuals and BANG! Lightbulbs everywhere.

7. x4

x4 works much the same way. Except for this time, we just double and double again.

Which for whatever reason, is really fun for my kids. 

I teach my kids (in addition and multiplication) to connect numbers with those triangle type things and put the answer underneath. This is useful when they are adding a lot of numbers because they can't keep all of those in their head (until later). 

8. Squared numbers

I put this one in because it's just FUN. My kids have practiced and practiced and practiced arrays. They understand that multiplication facts can be expressed in rectangles (rows and columns). So, I challenge them to find all the multiplication facts that make SQUARES. We use inch tiles to do this. Kids think all the even numbers are going to produce squares and quickly debunk that theory. At the end, students generate the list - 1, 2, 4, 9, 16, 25, etc.

I tell my kiddos that these are called (you'll never remember it, it's SO hard) - Square numbers (my kids didn't fall for this...I use it too much..)

 I usually write these on the board (1x1, 2x2, 3x3, etc). I teach my kids that when someone wants you to square something, you need to multiply it by itself. The answer will always be a square number.

It's a good concept for kids to understand and buys me a day before getting into dreaded x6.

9. x6

Times 6 is just. plain. hard. There's little way around it. Hopefully, kids can use one of the other tricks to find the problem but that still leaves 6x7 and 6x8 (7x6 and 8x6). ARGH!

There are two ways people teach the x6 strategy.

Double, double, double

OR

triple, triple (double, one more and double, one more)

If your students are master doublers or master triplers I would go with whichever one you think would work for them. Again, this one takes a LOT of modeling and visuals. SHOW students how 6 can be broken into the 2 groups of 3 or 3 groups of 2. 

10. x8

Double, double, double, double? YIKES.

Important to note that for x7 and x8, students will need automaticity of smaller facts they can use. For example, x8 can become x4+x4 or x5 + x3!

11. x7

x6 and 1 more group

OR

just use the other number's strategy (my go to! lol)

I have noticed a tremendous improvement in my students' multiplicative skills through explicit instruction of STRATEGIES.

Now you're going to have to remember like any other skill students need a lot of time to internalize these strategies. It may seem like it's just faster to have them memorize them and whip those flashcards out. BUT, our ultimate goal for our math students should be solid conceptual understanding. We should strive for them to have lifelong skills that rely on number sense, help them think flexibly, and make SENSE!

How do we do it? One strategy at a time. It's very helpful to create a chart for every strategy. Students can keep these, physically in a notebook or digitally, and refer to them when they get stuck.

Fortunately, I have all the charts ready to go for you!

Every chart has a space for the strategy, facts, and a word problem!

Happy teaching!